Recall that Regular Reader Jon (“The Unknown”) asked: “If I start from my house in Vancouver and fly NE, keeping my plane flying in a straight line, what country do I next enter?”
As it turns out, Jon tU lives very near to Vancouver, BC. So I’ve modified his question just a bit to make it just a tad simpler. (And for these Challenges, you can safely ignore all weather issues, magnetic anomalies, and forbidden flying zones… )
Here’s the start of Jon’s hypothetical flight path:
And our questions:
1. If Jon flies from the Vancouver, BC, airport on a NE heading, and flies in a straight-line, swerving neither to the left or the right, what’s the next country he’ll fly over? (And for extra credit, what’s the name of airport he should land at?)
The answer that several people gave was to look at a map (e.g., Google Maps), draw a NE line and look to see the next country that it crosses, like this:
The problem is that we live on a sphere, and straight lines on the map turn into giant curves in reality.
One way to look at this is to get a globe (yes my friends, a physical device with a map of the planet impressed on the surface), take a piece of string, and try to see where a straight flight NE out of Vancouver would take you. I asked Gary Marchionini (the Dean of the School of Information and Library Science at the University of North Carolina at Chapel Hill) if I could borrow one. Luckily, he happened to have one at home (because they don’t seem to exist in libraries any more), and we gave this course calculation a try. Starting with one end of the string in Vancouver, we stretched it in a due NE direction:
Here you see me trying to stretch a string NE from Vancouver in a straight line. As you can see in the left image, the string just barely intersects the bottom end of Greenland. But in the pic on the right, a slight adjustment of the string has it hitting the corner of Spain and Portugal and missing Greenland.
This is obviously too coarse a measurement, but it shows the point nicely: A straight line on a Mercator projection map (e.g., the Google Map above) is a serious distortion.
The path the string follows is… what? Let’s figure this one out. Obviously, we need to understand a bit about lines-on-a-sphere:
[ straight lines on a sphere ]
tells us that “straight lines on a sphere are Great Circle lines…” Ah, that’s right. Now I remember my high school geometry–if you fly on a straight line across the globe, you’re actually on a Great Circle route! (That is, if you start on a NE heading from Vancouver, and fly long enough, you’ll end up back in Vancouver–it’s a circle on the globe.)
So NOW our question is “what Great Circle is at 45 degrees (NE)?” How do we find that?
When I asked Jon (the Unknown) this question he wrote back that he needed to first understand waht a “NE heading” really means. As he found, it means..
We first need to define ‘azimuth’ as a way to define what a ‘heading” is. The azimuth is the angle between the north vector and the perpendicular projection of the star down onto the horizon. (If you do a query like [ define azimuth ] you’ll learn that it’s the direction of a celestial object from the observer, and expressed as the angular distance from the north or south point of the horizon to the point at which a vertical circle passing through the object intersects the horizon.
That is, it’s the horizontal angle or direction of a compass bearing from a pooint. Azimuth is usually measured in degrees. The concept is used in navigation and astronomy.
This means I need to follow the initial azimuth line from CYVR (Vancouver airport code) at an heading of 45 degrees; that’s NE.
A search for:
[how to draw a great circle route]
finds many tools, including the Great Circle Mapper which will draw it for you if you have a beginning and end point. But so far we don’t have an end point. so I used the Mapping and Distance Tools (at ACSCDG.com) which allows a starting point, and asks for a route option for which I drew a line in the general direction NE.
In the box to the left of the map is a table which shows azimuth and distance. I kept shrinking the map to show CYVR and Europe and with a heading (azimuth) of 45, which draws a nice red line showing the Great Circle route:
 |
| The data table from ACDCDG showing the azimuth and distance traveled, starting at the Vancouver airport and landing in Spain. |
This neatly and easily drew a nice red line which just missed Greenland and then made a solid hit by Porto (OPO) in Portugal.
When I did this (Dan), I found that the Great Circle route definitely misses Greenland (but just barely), but it actually hits Spain first, just a few miles north of the Portugal border.
 |
| When you zoom in, you’ll see the NE azimuth heading from Vancouver airport hits Spain, near the border with Portugal. |
If you do this same Great Circle Route calculation from his hometown of Courtenay, which is just a bit north of the Vancouver airport, you can see I got slightly different results:
 |
| This was Jon’s route calculation starting from Courtenay. |
Just to check, if you go back to the other tool (Great Circle Mapper), and put in Vancouver for one end, and Porto (Portugal) at the other end, you’ll see this map:
The initial heading here is 46 degrees (because we’re asking for the YVR to OPO (Porto) route–not the route to “first landfall outside of Canada” as I did in my computation from Vancouver airport).
So the answer is… Spain (if you start from Vancouver Airport) OR Portugal (if you start at Jon’s hometown of Courtenay).
But we also have the mileage… 5,045 miles. Which will be handy for our next question…
2. If Jon is flying an Airbus A340-200, about how long will the flight take? (Again, ignore weather, headwinds, tailwinds, etc.)
After all of that map stuff, this is easy. The query:
[ A340-200 range airspeed ]
leads us to the Airbus website, which tells us that “…optimal range of 6,700 nautical miles..” and that the cruising speed is 537 mph (867 kph) at 36,000 feet (11,000 m). A quick Google query for:
[ 5045 /537 ] = 9.39 (hours)
tells us that this is about a 9.4 hour flight.
3. What distance is it from Vancouver to this mysterious destination’s biggest airport (that is, where can he safely land his Airbus A340-200 in that country)?
What about that airport near the place where the Great Circle hits–Porto?
[ Porto airport ]
The Wikipedia entry tells us that the runway there is 11,417 feet long (3,480 m). Searching for:
[ A340-200 landing distance ]
tells us that the takeoff/landing distance required varies from 2990m – 3100 m (takeoff), 1890m – 2100m (landing), depending on load and conditions. (Data aggregated from a number of different sites.)
And so, yes, Jon can land his A340-200 at Porto, Portugal.
4. Can he make it there without refueling?
As we found earlier, the range of the A340-200 is 6,700 nautical miles. But notice that the distance was given in regular miles. Are we really okay?
The Google query to do conversions can be done like this:
[ 5,045 miles in nautical miles ]
We can see that this is easily within the range limit we found above.
Search Lessons
This Challenge certainly generated a few great search lessons.
1. Be aware of the context of the question. In this case, the context is literally global. You might have picked up from the odd phrasing of the question that something was up. If Jon flies on a “…NE heading, and flies in a straight-line, swerving neither to the left or the right, what’s the next country he’ll fly over?” Pay attention to the details of the question (“… NE heading”), and realize that this is a flight heading on a sphere. Unless you have incredible spatial reasoning, you probably won’t be able to intuit what the answer is, and so you have to do some background searches to learn about azimuth, Great Circle routes, and so on.
2. Look for tools to do the work for you. Since we learned that Great Circle routes are involved here, you should take a minute to check for mapping tools to help with this Challenge. Luckily, there are several Great Circle mapping tools, and we can use them to our advantage.
3. Remember the conversion / calculator tools and pay close attention to units that you’re finding in the text.
For Teachers
These kinds of questions can be really challenging for students who might not realize that different map projections have very different properties. It’s one of those cases where a simple question can lead to lots of geography and mapping exercises. (And, if your students are really advanced, some spherical geometry. See the Wikipedia page on Spherical Geometry to learn how to compute angles of geodesic lines on a sphere.)
On the other hand, mapping Challenges can be very compelling for students, especially if you can link it to personal connections (such as where their ancestors came from originally, local sports figures, etc.).
And, if you want to pursue the Great Circle Challenge, consider this question: Can your students find the shortest path from Melbourne to Rio de Janeiro? If they do, what continents does the path cross? (The answer is pretty surprising!)
Postscript: Another solution
As I was working on this Challenge, I remembered that there was a “geodesic preserving map projection,” but I couldn’t remember much about it. The one thing I DID remember was that a Great Circle route would show up as a straight line. (A “geodesic” is the same as a Great Circle route on a sphere.) So I did the obvious query:
[ geodesic preserving map ]
and found that this kind of map is always centered on a particular location (say, Vancouver), and that straight lines from the center can be used to figure what the Great Circle route heading off at 45 degrees to the NE. I also learned it’s called an azimuthal stereographic projection. These are circle-preserving, as any circle upon the sphere (every geodesic, parallel and meridian) is mapped to a circle; and where geodesic lines crossing the central point map to circles with infinite diameter–in other words, straight lines.
Following my own advice, I searched for a tool to do this:
[ azimuthal projection map generator ]
which led me to a generator. If you drop in the lat/long for Vancouver airport, you’ll create this map:
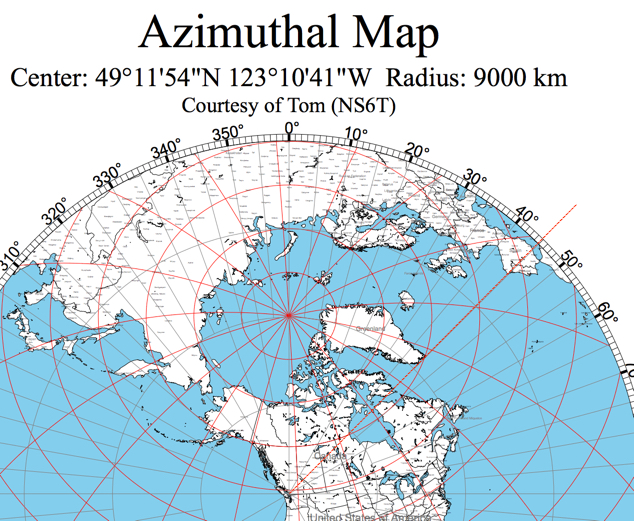 |
| Azimuthal map projection centered on Vancouver. Map generated by NS6T.net I added the extra red line at the NE azimuth (45 degrees) |
As you can see, this gives us the same answer as we found earlier–it just misses Greenland and intersects Europe right at the junction of Portugal and Spain.










